Utilização da integral definida de 1/t para estimar a série harmônica

Dedução da fórmula do centro de massa de uma haste fina a partir de sua função de densidade linear.

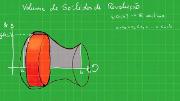
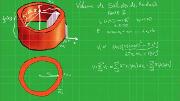
Outra aplicação das integrais, encontrando uma fórmula para o comprimento do gráfico de uma função. A fórmula é deduzida aproximando o gráfico da função por uma curva poligonal, isto é, uma curva formada por segmentos de reta. O comprimento desta curva poligonal nada mais é que a soma de Riemann de uma certa função. Quando a norma da partição tende a zero obtemos a fórmula exata do comprimento do gráfico.

Dedução de uma fórmula para o volume de um sólido de revolução definido pela rotação do gráfico de uma função no plano xy em torno do eixo x. Para este fim aproximamos o sólido por uma união de cilindros cujas bases são discos.

Dedução de uma fórmula para o volume de um sólido de revolução aproximando o volume do sólido pelo volume de uma união de cascas cilíndricas e então tomando o limite quando a norma da partição envolvida converge para zero

Cálculo da derivada da função x ao quadrado, f(x)= x*x, em qualquer ponto x, fazendo uso da definição da derivada como o limite dos quocientes de Newton da função f no ponto x.

Verificação da função f(x)= cos(x) como diferenciável e demonstração de sua derivada f'(x)=-sen(x) em qualquer ponto x, fazendo uso da definição da derivada como o limite dos quocientes de Newton da função f no ponto x. Uso da conhecida identidade trigonométrica que expressa o cosseno da soma de dois ângulos em termos dos senos e cossenos de cada ângulo.

Calculamos a integral de exp(t) no intervalo [0,x] utilizando a definição de integral definida via somas de Riemann e alguns fatos básicos sobre a função exponencial.

Nós observamos primeiramente que toda função contínua em um intervalo [a,b] é integravél. Depois calculamos, via limite de somas de Riemann, a integral da função f(x)=x em um intervalo da forma [0,b]. O argumento é bem interessante, fazendo uso de uma curiosa fórmula para a soma de todos os números naturais de 0 até k.

Cálculo do limite de uma função racional bem simples, cujo denominador é uma função afim e o numerador é uma função quadrática. Exemplo em que o denominador da função se anula no ponto limite, de modo que não se pode utilizar aqui a regra do quociente.